Research Pillars

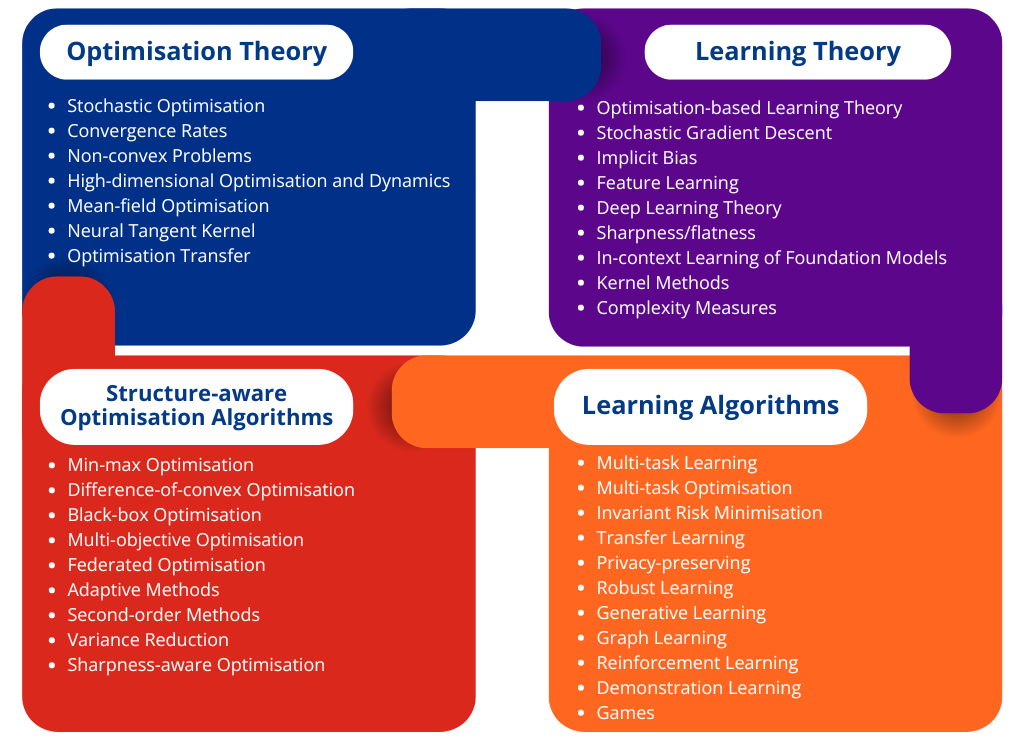
Theory and Optimisation in AI

Artificial intelligence has achieved remarkable success in many tasks, such as object and speech recognition, game AI, robot control, drug discovery, molecule design, and foundation models. This success is attributed to massive datasets, huge computational resources, and the great expressive power of high-dimensional models such as deep neural networks. However, building a large model on a massive dataset entails significant costs. Hence, reducing the required amount of data and compute remains an imperative research direction. In short, the next generation learning methodologies must be:

Optimisation forms the foundation of many AI applications, as training AI models is essentially similar to solving a high-dimensional optimisation problem. Hence, improving optimisation performance and analysing its behaviour could directly bring the above features to many learning methodologies.

Optimisation-based Learning Theory

While overparameterised models, such as deep neural networks, offer many solutions that fit the training dataset, their generalisation capabilities can vary. As the nature of the solution obtained is dependent on the optimisation method, all aspects, including optimisation, modelling, and regularisation need to be studied comprehensively to understand the mechanism behind modern AI systems. Through optimisation-based learning theory, we aim to understand the reasons behind the superior performance of deep learning, including its high prediction accuracy, exceptional adaptability of foundation models to downstream tasks, and ability to perform in-context learning.

Learning problems often exhibit special problem structures depending on their purpose and context. Therefore, it is important to design optimisation methods that utilise these structures to enhance performance.

Here, we focus on the following research areas:

Black-box optimisation

Black-box optimisation targets the problem that only supports function query access without the actual gradient. It has many applications, including prompt fine-tuning in large language models, automatic hyper-parameters tuning in AI models, material design, drug discovery, robotic control, etc. We aim to develop efficient black-box optimisation algorithms with theoretical convergence guarantees, such as Bayesian optimisation, stochastic zeroth-order optimisation, model-based optimisation, and multi-objective black-box optimisation. Furthermore, we will apply these algorithms to solve the practical problems listed above.

Multi-task learning

Multi-task learning aims to solve multiple tasks with the use of a single model. By jointly training multiple correlated tasks, it acquires common features between those tasks and improves the generalisation ability for each task. For example, it can simultaneously solve classification, object detection, and segmentation tasks on image datasets while solving multilingual translation, text summarisation, and question-answering tasks on text datasets. One approach for multi-task learning involves formalising it as multi-objective optimisation problems. By leveraging this problem structure, we study multi-task optimisation methods for multi-task learning.

Transfer Optimisation

Transfer Optimisation leverages common knowledge among multiple problems. Although real-world problems seldom exist in isolation, it is common for optimisation solvers to run from scratch without prior knowledge about the task. To address this, we aim to develop a method that automatically transfers knowledge across problems to accelerate convergence.

In addition to the above, we study the following research topics to develop theoretically grounded data- and resource-efficient optimisation methods applicable to various problems:

We will also explore various applications with the goal of making significant impact across a wide range of scientific fields. For instance, one objective is to provide guidelines for training and fine-tuning foundation models through theoretically grounded learning methodologies. Consequently, this approach could streamline the training of foundation models and reduce the significant costs required.

A*STAR celebrates International Women's Day

A*STAR Women In Science

From groundbreaking discoveries to cutting-edge research, our researchers are empowering the next generation of female science, technology, engineering and mathematics (STEM) leaders.

Get inspired by our #WomeninSTEM