Quantum Computing
Background / Motivation
Quantum computers have the potential to produce tremendous improvements in computational performance for a wide range of problems in various fields, including optimisation, machine learning, chemistry, finance, and healthcare. As the performance of quantum hardware improves, so does the possibility of implementing quantum algorithms that outperform their classical counterparts. There is currently an ongoing race amongst various academic research groups, companies, and national research labs to produce the first demonstration of a practical quantum advantage – a milestone in which a quantum computer solves a problem of practical interest with a performance that classical computers cannot match.
Such a demonstration would involve:
1) using actual quantum hardware to run such a quantum algorithm,
2) showing that classical computers cannot perform as well.
At IHPC, we take a holistic hardware-agnostic full-stack approach that aims to harnesses the power of quantum computers to produce a practical quantum advantage. We aim to develop end-to-end full-stack solutions that bridge the gap between end-users problem statements and quantum-accelerated solutions optimally deployed on near-term quantum hardware by leveraging our existing expertise in HPC modelling and simulations and AI, as well as our vibrant developments in the field of quantum computing.
Together with the Centre for Quantum Technologies (CQT) at the National University of Singapore and the National Supercomputing Centre (NSCC) Singapore, IHPC is also a founding member of the National Quantum Computing Hub (NQCH), one of the three national platforms launched by Singapore's Quantum Engineering Programme (QEP), focusing on developing quantum computing capabilities and exploring applications through industry collaborations. IHPC will contribute our expertise in computational science, high performance computing, artificial intelligence and optimisation to this ecosystem effort. This will include work on algorithms and middleware for academia and industry applications.
Capabilities
Quantum computers have the potential to produce tremendous improvements in computational performance for a wide range of problems in various fields, including optimisation, machine learning, chemistry, finance, and healthcare. As the performance of quantum hardware improves, so does the possibility of implementing quantum algorithms that outperform their classical counterparts. There is currently an ongoing race amongst various academic research groups, companies, and national research labs to produce the first demonstration of a practical quantum advantage – a milestone in which a quantum computer solves a problem of practical interest with a performance that classical computers cannot match.
Such a demonstration would involve:
1) using actual quantum hardware to run such a quantum algorithm,
2) showing that classical computers cannot perform as well.
At IHPC, we take a holistic hardware-agnostic full-stack approach that aims to harnesses the power of quantum computers to produce a practical quantum advantage. We aim to develop end-to-end full-stack solutions that bridge the gap between end-users problem statements and quantum-accelerated solutions optimally deployed on near-term quantum hardware by leveraging our existing expertise in HPC modelling and simulations and AI, as well as our vibrant developments in the field of quantum computing.
Together with the Centre for Quantum Technologies (CQT) at the National University of Singapore and the National Supercomputing Centre (NSCC) Singapore, IHPC is also a founding member of the National Quantum Computing Hub (NQCH), one of the three national platforms launched by Singapore's Quantum Engineering Programme (QEP), focusing on developing quantum computing capabilities and exploring applications through industry collaborations. IHPC will contribute our expertise in computational science, high performance computing, artificial intelligence and optimisation to this ecosystem effort. This will include work on algorithms and middleware for academia and industry applications.
Our focus are:
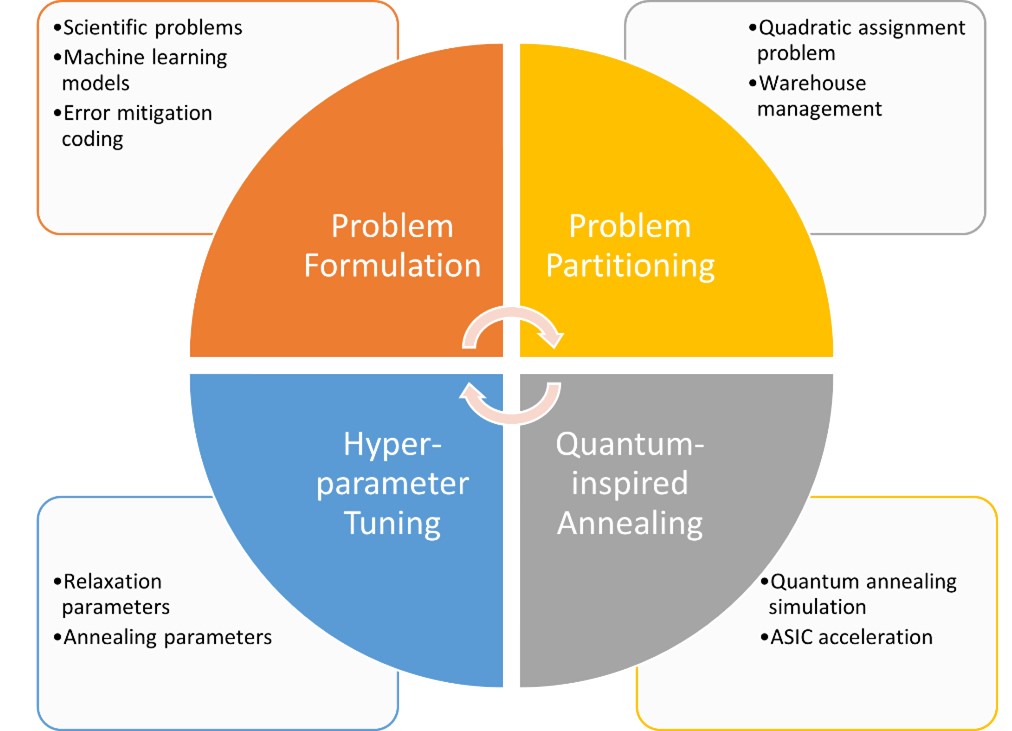
Simulations
- Quantum simulations of many-body quantum physics in chemistry, materials, and quantum optics
- Linear systems and differential equations in fluid dynamics, electromagnetism, and solid mechanics
Optimisation
- Gate and annealing-based optimisation
- Quantum-inspired annealing-based optimisation
- Operation research and structure optimisation
- Optimisation for AI/ML
Quantum Control and Readout
- Pulse-level programming
- Optimal control protocol for noise reduction
- Hardware characterisation via AI/ML
The horizontal efforts to understand the power and limitations of near-term quantum computers and to lower the entry barrier of quantum computing are:
- Quantum algorithms
- Quantum complexity
- Quantum error mitigation
- Benchmarking against classical algorithms and HPC, and cross-quantum-devices
- Full-stack software engineering and workflow developments
Collaboration Opportunities
IHPC welcomes interested parties to collaborate in research and development relating to Quantum Computing, especially in identifying new technology areas to develop new applications, multi-disciplinary projects, or commercialisation outcomes.
For more info or collaboration opportunities, please write to enquiry@ihpc.a-star.edu.sg.
IHPC welcomes interested parties to collaborate in research and development relating to Quantum Computing, especially in identifying new technology areas to develop new applications, multi-disciplinary projects, or commercialisation outcomes.
For more info or collaboration opportunities, please write to enquiry@ihpc.a-star.edu.sg.
A*STAR celebrates International Women's Day

From groundbreaking discoveries to cutting-edge research, our researchers are empowering the next generation of female science, technology, engineering and mathematics (STEM) leaders.
Get inspired by our #WomeninSTEM
.png?sfvrsn=ff199933_15)